What is a Tessellation?

The words tessellate and tessellation come from a Latin word which means "small

stones" and "to pave with small stones". A tessellation or tiling is a group of polygons

or tiles that have non-overlapping congruent sides and these tiles completely cover the

plane with no holes.

A Greek mathematician named Zenodorus (200 B.C.) discovered that regular

polygons (polygons with congruent sides) enclosed the greatest area. Around 300 A.D.,

Pappus expanded the discovery of Zenodorus. Pappus gave an example of honeybees.

Pappus believed that bees made their honey exclusively for human consumption. For this

reason, bees needed to store their honey in a way in which none would be wasted.

A proposition came from Pappus’ belief about the bees. It states "There are only three

ways to arrange identical regular polygons about a common vertex without interstices".

n being the number of sides in the regular polygon.

with n = 3.

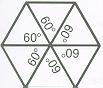
1) "If n = 3, each polygon is an equilateral triangle with 60 degrees per

angle. We can put 360 degrees/60 degrees = 6 equilateral triangles to-

gether at each vertex without gaps."(Dunham, pg. 110)(Ranucci, pg. 16)

2) "If n = 4, each polygon is a square with 90 degrees per angle. We

can clearly assemble 360 degrees/90 degrees = 4 squares at each vertex."

(Dunham, pg. 111) (Ranucci, pg. 16)

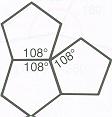
3) "For n = 5, we have seen that each angle of a regular pentagon con-

tains 108 degrees. But 108 degrees does not go evenly into 360 degrees,

as 360 degrees/108 degrees = 3 1/3. Thus, regular pentagons cannot fill

all space about a point without leaving gaps."(Dunham, pg. 111)(Ranucci, pg 16)

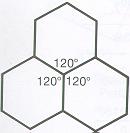
4) "For n = 6, we have a regular hexagon. Each interior angle contains

120 degrees and so we can assemble 360 degrees/120 degrees = 3 hexagons at each vertex."(Dunham, pg. 111)(Ranucci, pg. 16)

The two discoveries that occurred with Zenodorus and Pappus are some of basic

concepts that help explain why tiling works.

The first mathematician to use tiling in geometry was Johann Kepler (1571 –

1630). He discovered in 1619 that there are only three regular polygons that will

tessellate. They are 1) equilateral triangle, 2) square, and 3) regular hexagon. He also

discovered a tiling that included a regular pentagon, decagon, "fused"

double decagon, and five-pointed star.

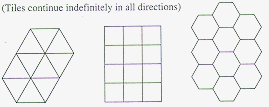
We will now look at different types of tessellations that deal with regular

polygons. Let us first look at the three regular polygons that tessellate by themselves. These are equilateral triangle, square, and regular hexagon.(Kay, pg. 245)

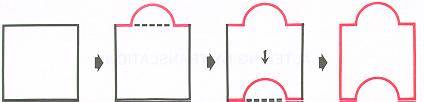
We now can change these regular polygon shapes by translating, rotating, and

reflecting them. We will first start with translating a square. By translating, we make a

change to one side, then we also make the same change to the opposite side. Here are a couple of examples.(Rannucci, pg. 40) (Ranucci, pg. 49)

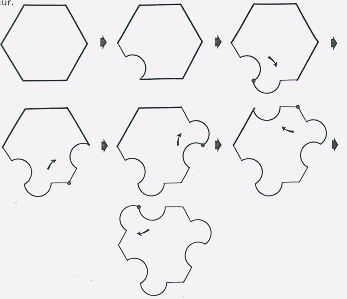
We can take a regular hexagon and translate the sides to form a different shape. (Ranucci, pg. 54) (Ranucci, pg. 55)

In all of these translations, the area in the finished figure is equal to the area that the regular polygon started with. For example, if the square that we worked with in the first translation had an area of 2 units, then the translated figure wou ld also have an area of 2 units.

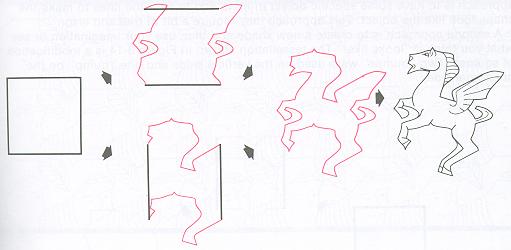
We will now take a look at rotation. Since we are changing a side and then rotating that side with its endpoint, we have to look at figures that have at least two congruent adjacent sides. These figures include an equilateral and isosceles triangles, a square, a rhombus, a kite, and a regular hexagon. But we are limiting this section to regular polygons. We will look at an equilateral triangle, a square, and a regular hexagon. (Ranucci, pg. 64) (Ranucci, pg. 68) (Ranucci, pg. 78)

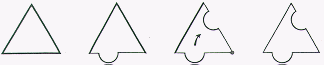
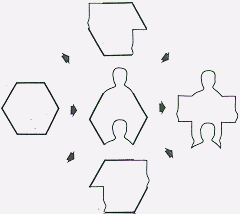
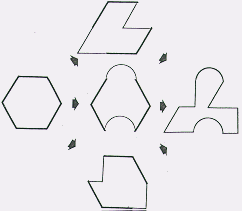
We will now look at reflections. A reflection by itself will not tessellate. But if you reflect and rotate your shape, it will tessellate with its self and its reflection.(Ranucci, pg. 111)

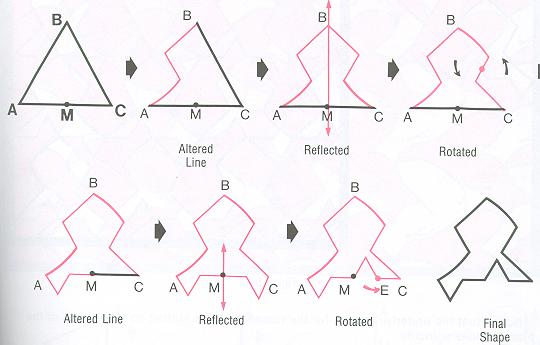
In the example above, we see an alteration, a reflection, and a rotation to an equilateral triangle. When the new shape is put into the plane, the original and the it’s reflection are needed to tile the plane.This section has briefly covered tessellati ons and the mathematics in tessellating.

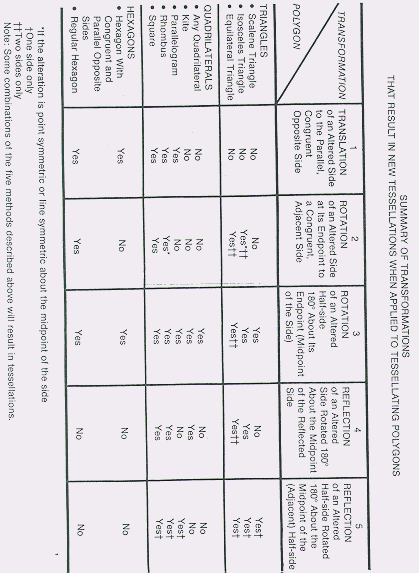
The following chart (Ranucci, pg.119) gives an overview of different polygons.

BIBLIOGRAPHY

Dunham, William, The Mathematical Universe. New York, John Wiley and Sons, Inc,

1994.

Kay, David C., College Geometry A Discovery Approach. New York, Harper Collins

College Publishers, 1994.

Ranucci, E.R., Creating Esher-Type Drawings. California, Creative Publications, 1977.

Usiskin, Zalman, Geometry. California, Scott Foresman and Company, 1997.